Svenska:
Den här webbplatsen kan endast nås som arkivreferens. De officiella webbsidorna för avdelningen för partikelfysik finns på http://particlephysics.physics.lu.se
Sidan nedan slutar uppdateras fr.o.m. 2020-09-22 och uppfyller endast delvis tillgänglighetsdirektivet. Se tillgänglighetsredogörelsen
English:
The webpage you reached is made available for archiving purposes only. The official division of particle physics webpages can be found at http://particlephysics.physics.lu.se
The page below is not updated any longer since September 22, 2020 and does not conform completely to the accessibility regulation. See the accessibility statement




Next: Cut-map Efficiency
Up: -Collision Data
Previous: -Trigger
Expected number of
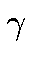
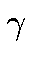 -Events
-Events
The expected
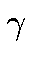
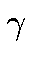 -signal is extracted as the total
number of events seen minus the expected background. There are two
different ways to classify the total number of single and double
tags. Either a trigger is accepted if there is nothing else in the
other modules, or an event is tagged regardless of what is seen in
the other VSAT modules.
-signal is extracted as the total
number of events seen minus the expected background. There are two
different ways to classify the total number of single and double
tags. Either a trigger is accepted if there is nothing else in the
other modules, or an event is tagged regardless of what is seen in
the other VSAT modules.
The first method should be used if the physics in single tag
events should be studied, as the second electron then is assumed
to go in the beampipe with
Q2 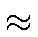 0. In this analysis the
single tag events are mainly used to extract the expected size of
the
0. In this analysis the
single tag events are mainly used to extract the expected size of
the
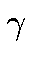
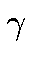 -signal, therefore the second method is to prefer.
-signal, therefore the second method is to prefer.
The expected background can easily be extracted as the off-energy
background probability times the number of notag events, as
explained in section 3.3. This gives the correct value
within 5-10%, due to systematical errors and off-energy
background fluctuations over the data taking period. Therefore
other methods of measuring the off-energy background also had to
be adopted in order to get the best possible background
estimation. In this analysis the background also was adjusted to
the following measurements:
- The ratio of the number of
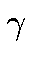
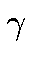 events between the
modules fluctuates with the beamspot position, but should be quite
stable for a whole data taking period.
events between the
modules fluctuates with the beamspot position, but should be quite
stable for a whole data taking period.
- The relative number of recorded events should correspond to
the relative luminosity.
- By adjusting the size of the cut maps and compare the impact
on data, background and
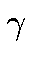
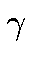 -Monte Carlo, it is possible
to extract the expected background [18].
-Monte Carlo, it is possible
to extract the expected background [18].
- The energy distribution of the data should be comparable to
that of the Monte Carlo, or at least the same for all
modules. The off-energy background and
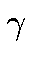
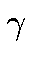 energy
distribution look quite different, so a change in the size of the
subtracted background will directly reflect in the final energy
distribution.
energy
distribution look quite different, so a change in the size of the
subtracted background will directly reflect in the final energy
distribution.
Taking these measurements into account, the off-energy background
probability obtained from STIC and VSAT Bhabha measurements could
be fine tuned. Once the expected number of background events
(Table 3.1) have been obtained, the
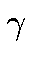
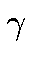 -signal is extracted as the remaining part of the
data. This is presented in table 5.1 along with the
probability to have a single tag event, when the hadronic system
is triggered.
-signal is extracted as the remaining part of the
data. This is presented in table 5.1 along with the
probability to have a single tag event, when the hadronic system
is triggered.
Table 5.1:
The expected number and probability(in %) of
single tag
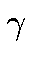
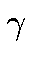 -events.
-events.
| |
Module 1 |
Module 2 |
Module 3 |
Module 4 |
| Energy |
Events |
Prob. |
Events |
Prob. |
Events |
Prob. |
Events |
Prob. |
| 189 |
2571 |
0.81 |
2234 |
0.71 |
2177 |
0.69 |
2290 |
0.72 |
| 192 |
415 |
0.73 |
360 |
0.64 |
347 |
0.61 |
369 |
0.65 |
| 196 |
1405 |
0.81 |
1216 |
0.71 |
1179 |
0.68 |
1252 |
0.73 |
| 200 |
1447 |
0.78 |
1250 |
0.67 |
1199 |
0.64 |
1277 |
0.69 |
| 202 |
678 |
0.74 |
584 |
0.64 |
569 |
0.62 |
599 |
0.65 |
| 206 |
2558 |
0.73 |
2288 |
0.65 |
2187 |
0.62 |
2348 |
0.67 |
| TOT |
9073 |
0.77 |
7932 |
0.67 |
7659 |
0.65 |
8135 |
0.68 |
|
If the two photons in a
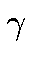
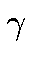 collision were totally
independent, the probability for a double tag would just be the
joint combination of two single tags. The cuts on the particle
system do however relate the two electrons and thereby increases the
double tag probability. The expected number of double tags is
therefore extracted by partly looking on the double tag data when
the expected background has been subtracted and partly on the
probability of a single tag [18]. This is presented in table
5.2 along with the Monte Carlo expectations.
collision were totally
independent, the probability for a double tag would just be the
joint combination of two single tags. The cuts on the particle
system do however relate the two electrons and thereby increases the
double tag probability. The expected number of double tags is
therefore extracted by partly looking on the double tag data when
the expected background has been subtracted and partly on the
probability of a single tag [18]. This is presented in table
5.2 along with the Monte Carlo expectations.
Table 5.2:
The expected number of double tag
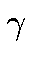
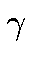 -events for different module combinations and the total sum compared with Monte Carlo
-events for different module combinations and the total sum compared with Monte Carlo
| Energy |
1+4 |
2+3 |
1+3 |
2+4 |
Tot |
MC |
|
|
| 189 |
27 |
22 |
26 |
22 |
97 |
92 |
|
|
| 192 |
4 |
3 |
4 |
3 |
14 |
16 |
|
|
| 196 |
15 |
12 |
14 |
12 |
53 |
48 |
|
|
| 200 |
14 |
11 |
14 |
12 |
51 |
52 |
|
|
| 202 |
6 |
5 |
6 |
5 |
23 |
25 |
|
|
| 206 |
24 |
20 |
23 |
21 |
89 |
93 |
|
|
| Tot |
90 |
74 |
87 |
75 |
326 |
327 |
|
|
|




Next: Cut-map Efficiency
Up: -Collision Data
Previous: -Trigger
Andreas Nygren
2001-10-24
![]()
![]() -signal is extracted as the total
number of events seen minus the expected background. There are two
different ways to classify the total number of single and double
tags. Either a trigger is accepted if there is nothing else in the
other modules, or an event is tagged regardless of what is seen in
the other VSAT modules.
-signal is extracted as the total
number of events seen minus the expected background. There are two
different ways to classify the total number of single and double
tags. Either a trigger is accepted if there is nothing else in the
other modules, or an event is tagged regardless of what is seen in
the other VSAT modules.
![]() 0. In this analysis the
single tag events are mainly used to extract the expected size of
the
0. In this analysis the
single tag events are mainly used to extract the expected size of
the
![]()
![]() -signal, therefore the second method is to prefer.
-signal, therefore the second method is to prefer.
![]()
![]() -signal is extracted as the remaining part of the
data. This is presented in table 5.1 along with the
probability to have a single tag event, when the hadronic system
is triggered.
-signal is extracted as the remaining part of the
data. This is presented in table 5.1 along with the
probability to have a single tag event, when the hadronic system
is triggered.
![]()
![]() collision were totally
independent, the probability for a double tag would just be the
joint combination of two single tags. The cuts on the particle
system do however relate the two electrons and thereby increases the
double tag probability. The expected number of double tags is
therefore extracted by partly looking on the double tag data when
the expected background has been subtracted and partly on the
probability of a single tag [18]. This is presented in table
5.2 along with the Monte Carlo expectations.
collision were totally
independent, the probability for a double tag would just be the
joint combination of two single tags. The cuts on the particle
system do however relate the two electrons and thereby increases the
double tag probability. The expected number of double tags is
therefore extracted by partly looking on the double tag data when
the expected background has been subtracted and partly on the
probability of a single tag [18]. This is presented in table
5.2 along with the Monte Carlo expectations.