The
![]()
![]() -collision processes have for LEP II energies typically
cross sections that are two to three orders of magnitude larger than
e+e- annihilation processes [28]. The cross section for the
process
-collision processes have for LEP II energies typically
cross sections that are two to three orders of magnitude larger than
e+e- annihilation processes [28]. The cross section for the
process
![]()
![]()
![]() hadrons is extracted from the
measurement of
e+e-
hadrons is extracted from the
measurement of
e+e- ![]() e+e- + hadrons [29]:
e+e- + hadrons [29]:
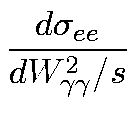 =
= 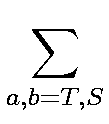
Here
d![]() is the measured cross section for the
e+e-
is the measured cross section for the
e+e- ![]() e+e- + hadrons reaction for a certain dW interval.
The center of mass energy is given by
e+e- + hadrons reaction for a certain dW interval.
The center of mass energy is given by ![]() and
and
![]() ab is the two photon luminosity function, which describes the
photon flux. Qi2 are the virtualities (momentum transfer in
the e
ab is the two photon luminosity function, which describes the
photon flux. Qi2 are the virtualities (momentum transfer in
the e![]() vertice) of the radiated photons. The hadronic cross
sections
vertice) of the radiated photons. The hadronic cross
sections
![]() correspond to specific helicity states
(T=transverse and S=Scalar) of the interacting photons. If
W2 > > Qi2 it is possible, to a very good approximation, assume
factorization of the Q and W dependencies of
correspond to specific helicity states
(T=transverse and S=Scalar) of the interacting photons. If
W2 > > Qi2 it is possible, to a very good approximation, assume
factorization of the Q and W dependencies of
![]() [30]:
[30]:
The functions ha, b are model dependent and describe the Q2
behavior of the hadronic cross section. If this is known it is
possible to extrapolate the
![]() (W
(W![]()
![]() 2, Q12, Q22) to Qi2 = 0 without
any loss of the W dependence. It is clear that the extrapolation
to Q2 = 0 is better for small values of Qi, which favor notag
data. At low Q2 most of the hadronic system is however lost in
the beampipe and the W measurement of notag data needs to be
unfolded with different MC simulations.
2, Q12, Q22) to Qi2 = 0 without
any loss of the W dependence. It is clear that the extrapolation
to Q2 = 0 is better for small values of Qi, which favor notag
data. At low Q2 most of the hadronic system is however lost in
the beampipe and the W measurement of notag data needs to be
unfolded with different MC simulations.
Double tag data do on the other hand provide an excellent W
measurement from the tagged electrons, and no model dependent
unfolding is needed. The extrapolated to Q2 = 0 is however
strongly model dependent for large Q2 values and this can
result in large uncertainties in the
![]() (W2)
measurement. The VSAT detector therefore has a unique advantage,
as is it can measure double tag events at low Q2 values.
(W2)
measurement. The VSAT detector therefore has a unique advantage,
as is it can measure double tag events at low Q2 values.