A hadron can be described by its parton contents, and as photons
fluctuate into partonic states a similar description can also be
adopted for the photon. The partonic content of a photon is
described by the photon structure functions, which is closely
related to the PDF's described previously. If one of the photons
in a
![]()
![]() -collision is almost on-shell with a
Q2
-collision is almost on-shell with a
Q2 ![]() 0, the whole process can be viewed as deep inelastic
scattering of the tagged electron off the quasi-real target
photon. The cross section can then be expressed as:
0, the whole process can be viewed as deep inelastic
scattering of the tagged electron off the quasi-real target
photon. The cross section can then be expressed as:
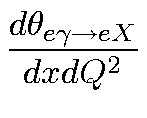 =
=
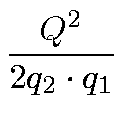
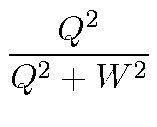 , y =
, y = 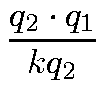
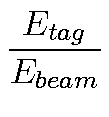 cos2(
cos2(
y is normally very small in the region studied, so it is only
possible to measure
F![]() 2. In the simple parton model
F
2. In the simple parton model
F![]() 2 is taken as a sum over the quark and antiquark
density functions. The Q2 evolution of these PDF's are
described by the Altarelli-Parisi equations. In case of the
photon, there is an extra term corresponding to a gamma going into
a q
2 is taken as a sum over the quark and antiquark
density functions. The Q2 evolution of these PDF's are
described by the Altarelli-Parisi equations. In case of the
photon, there is an extra term corresponding to a gamma going into
a q![]() pair. This renders the equations inhomogeneous and a
linear rise of
F
pair. This renders the equations inhomogeneous and a
linear rise of
F![]() 2 with ln(Q2) is expected. This was
seen by the LEP experiments, and is presented in Fig. 6.5.
2 with ln(Q2) is expected. This was
seen by the LEP experiments, and is presented in Fig. 6.5.
One of the more important results from HERA was the observed rise
of the proton structure function (Fp2) at low x-values. A
similar rise is also expected for the
F![]() 2 structure
function at very low x. Evidence for this is piling up from the
latest results (Fig. 6.6) of the LEP
experiments [27].
2 structure
function at very low x. Evidence for this is piling up from the
latest results (Fig. 6.6) of the LEP
experiments [27].