The pT cut-off

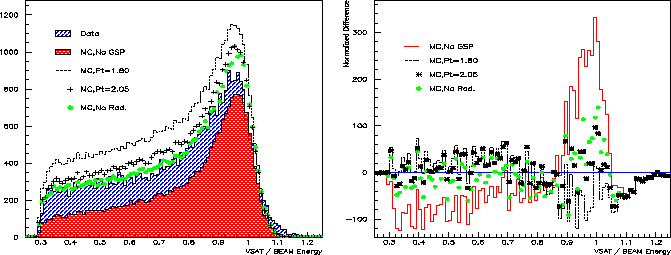
If the exact normalization of the MC was known it would be easy to find p_T^min, as the number of events in data and total MC would be equal. There is however a rather large (10-20%) uncertainty in the total cross section of the MC, so it would not be correct just to normalize the size of the data and MC with help of the p_T^min factor. Instead distributions of physical quantities sensitive to the QCD-RPC model have to be compared with data for the best fit of p_T^min. From Fig. 7.2 it is clear that the total energy distribution of the tagged electron will change with the p_T^min cut-off limit. This has been compared with data in Fig. 7.3 for three different values of p_T^min (There is in principle no QCD-RCP contribution for p_T^min greater than five).

**Figure 7.3:** The total energy distribution of MC with different values of p_T^min.
**Figure 7.4:** The normalized energy distribution for different values of p_T^min
$\begin{figure} \begin{center} \parbox {7.7cm}{ \centering\epsfig{file=phd-st_e.... ...ight=6cm,clip=,bbllx=10,bblly=10,bburx=530,bbury=530} }\end{center}\end{figure}$

It is clear that MC with p_T^min equal to 1.8 gives too many events and MC with no QCD-RCP contribution results in too few events. This could however be due to a bad normalization of the MC, so instead the normalized difference between data and MC was calculated in Fig. 7.4. Clearly the QCD-RCP contribution is needed in the MC, but the exact limit of p_T^min is hard to extract from this quantity.

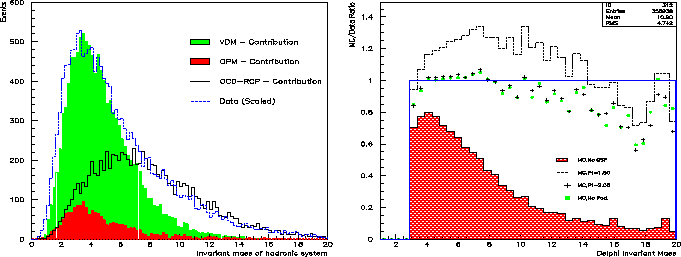
The invariant mass reconstructed from the hadronic system also differs for the three MC models (Fig. 7.5). The invariant mass can thus also be used to find the p_T^min cutoff limit. The ratio between the invariant mass distribution for data and MC is plotted in Fig. 7.6 for the same values of p_T^min as before.

The main bulk of events in Fig. 7.5 and 7.6 is between 3 and 10 GeV, so it is clear that p_T^min equal to 1.8 results in an excess of events and with no QCD-RPC contribution there are again too few events. The slope of the ratio is however more interesting to look at, as it should be more or less flat when a good agreement with data is found. A p_T^min cut at 2.05 seems to agree quite well with the data, and it is clear that the other two p_T^min limits can be excluded.

**Figure 7.5:** The invariant mass distribution for the different MC contributions. The distribution for data is also shown as a comparison.
**Figure 7.6:** The ratio of the invariant mass distribution for data and MC samples with different values of p_T^min (5.0, 2.05 and 1.8).
$\begin{figure} \begin{center} \parbox {7.7cm}{ \centering\epsfig{file=phd-mc_im... ...ight=6cm,clip=,bbllx=10,bblly=10,bburx=530,bbury=530} }\end{center}\end{figure}$

It is quite hard to distinguish the MC with or without radiative corrections, but it is clear that a p_T^min around 2.05 should be used. These results came from single tag data, which has small statistical error. The double tag data suffers from much larger statistical errors, but should also be checked for cross-reference. The number of accepted double tag events for different p_T^min limits can be found in table 7.2.

Table 7.2: The number of double tag events seen in data and in MC for different values of p_T^min.

Energy	Data	MC(p_T=1.8)	MC(p_T=5.0)	MC(p_T=2.05)	MC(2.05, NORAD)
189	97	110	57	93	79
200	140	174	72	141	127
206	89	118	49	93	88
TOT	326	402	178	327	294

The MC with p_T^min equal to 1.8 and 5.0 is as before too big and too small respectively. The MC with radiative corrections still agree very well with the data with a p_T^min equal to 2.05. The MC without radiative corrections is now however too small, with about 11% loss of events. As shown in section 7.2 there is no 200 GeV MC with radiative correction generated, so this was constructed by just up-scaling the 200 GeV MC without radiative correction with 11%.

Svenska:

English:

The p_T cut-off