Physics Motivation

Consider a scenario where a source emits particles with electric charge +1 and -1 with probabilities $p_+$ and $p_-$. In each event a fixed number of charged particles $n_{ch}=n_++n_-$ is emitted. The magnitude of the event-by-event fluctuations in charge $Q=n_+-n_-$ is calculated from the variance V$(Q)$.

$$\mt{V}(Q) \equiv \<Q^2\> - \<Q\>^2 =$$

$$= \<n_+^2\> + \<n_-^2\> - 2\<n_+n_-\> - \<n_+\>^2 - \<n_-\>^2 + 2\<n_+\>\<n_-\> =$$

$$= \mt{V}(n_+) + \mt{V}(n_-) - 2\mt{cov}(n_+,n_-) =$$

$$= 4p_+p_-\cdot n_{ch}$$ (13)

since, in this case, $\mt{V}(n_+) = \mt{V}(n_-) = p_+p_-n_{ch} = -\mt{cov}(n_+,n_-)$.

Different measures have been suggested for the study of net charge fluctuations. Since the variance of $Q$ scales with $n_{ch}$, one of the most simple choises is the normalized variance $v(Q)$, defined in the following way:

$$v(Q) \equiv \frac{\mt{V}(Q)}{\<n_{ch}\>}$$ (14)

Here the mean value of $n_{ch}$ is used, giving the possibility to study data samples containing events with varying $n_{ch}$.

Now consider the two scenarios of heavy-ion collisions illustrated in fig. 1.4. The purely hadronic scenario would very much resemble the example above, with the main charge carriers being pions. With $p_+=p_-=\htfrac12$ in (3.1) the normalized variance is simply $v(Q)=1$.

In a QGP, assuming thermal distributions ( $\mt{V}(n_{ch})=\<n_{ch}\>$) and no correlations,

$$\mt{V}(Q) \equiv \<Q^2\> - \<Q\>^2 = q_u^2\<n_{u+\bar{u}}\>+q_d^2\<n_{d+\bar{d}}\>$$ (15)

If the quark flavors appear with equal probability, the normalized variance is

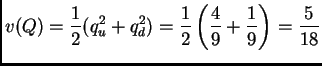$$v(Q) = \frac{1}{2} (q_u^2+q_d^2) = \frac{1}{2} \left(\frac{4}{9}+\frac{1}{9}\right) = \frac{5}{18}$$ (16)

This value is however not directly measurable in experiments. The essential question is whether the distribution of more evenly spread charge in a QGP survives the hadronization process, in order to be observed as a reduction in fluctuation.

Jeon and Koch have made a simple thermal model calculation to predict the magnitude of the fluctuations after hadronization [17]. They state a relationship between the number of created pions and the number of quarks and gluons inside the plasma:

$$\<n_\pi\> = \<n_g\> + \frac{4.2}{3.6}[\<n_{u+\bar{u}}\> + \<n_{d+\bar{d}}\>]$$ (17)

Using this result in (3.3), assuming that $\htfrac{2}{3}$ of the pions are charged, and that $\<n_{u+\bar{u}}\> = \<n_{d+\bar{d}}\> = \frac{1}{2}\<n_g\>$,

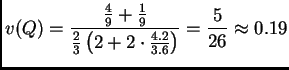$$v(Q) = \frac{\frac{4}{9}+\frac{1}{9}}{\frac{2}{3}\left(2+2 \cdot \frac{4.2}{3.6}\right)} = \frac{5}{26} \approx 0.19$$ (18)

A lattice calculation result of $v(Q)=0.25$ is also presented in [17], and it is argued that these reduced fluctuations should be seen in experiments.