Some Comparisons Between Various Measures

As was mentioned earlier several measures, along with $v(Q)$, have been suggested for characterizing the fluctuations. Here are the definitions of some of them. (The definition of $v(Q)$ is given once more for direct comparison.)

$$v(Q) \quad\equiv\quad \frac{\mt{V}(Q)}{\<n_{ch}\>}<tex2html_comment_mark>134$$ (32)

$$v(R) \quad\equiv\quad \mt{V}(R) \cdot \<n_{ch}\> = \mt{V}\left(\frac{n_+}{n_-}\right) \cdot \<n_{ch}\> \qquad \qquad \mt{\cite{jeon}}$$ (33)

$$\Gamma \quad\equiv\quad \frac{1}{\<n_{ch}\>}\left\<\left(Q-\frac{\<Q\>}{\<n_{ch}\>}n_{ch}\right)^2\right\> \qquad \qquad \mt{\cite{mrow}}$$ (34)

$$\nu_{dyn} \quad\equiv\quad \left\<\left(\frac{n_+}{\<n_+\>}-\frac{n_-}{\<n_-\>}\right)^2\right\> - \left(\frac{1}{\<n_+\>}+\frac{1}{\<n_-\>}\right) \qquad \qquad \mt{\cite{prun}}$$ (35)

In the stochastic scenario it was shown earlier that $v(Q)=1-\varepsilon^2$, independent of $n_{ch}$. However, $v(R)$ as a function of $n_{ch}$ suffers from a skewness. In the case where $\varepsilon=0$, $v(R)$ approaches the value 4 as $n_{ch}$ increases. For fixed $n_{ch}$ with $\varepsilon \neq 0$

$$\mt{V}(R) = \mt{V}\left(\frac{n_+}{n_-}\right) = \mt{V}\left(\frac{n_+}{n_{ch}-n_+}\right) = \mt{V}\left(\frac{n_{ch}}{n_{ch}-n_+}-1\right) =$$

$$= \mt{V}\left(\frac{n_{ch}}{n_-}\right) = n_{ch}^2 \cdot \mt{V}\l... ...c{1}{n_-}\right) \approx n_{ch}^2 \cdot \frac{1}{\<n_-\>^4} \cdot \mt{V}(n_-) =$$

$$= n_{ch}^2 \cdot \frac{1}{(p_-n_{ch})^4} \cdot p_+p_-n_{ch} = \fr... ...arepsilon)^4}{16}} = \frac{4}{n_{ch}} \frac{1+\varepsilon}{(1-\varepsilon)^3} =$$

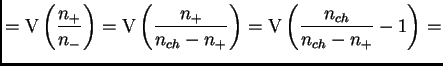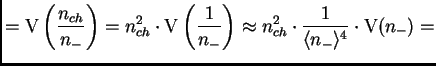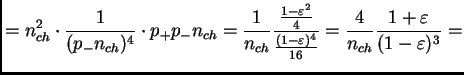$$= \frac{4}{n_{ch}} [ 1 + 4\varepsilon + O(\varepsilon^2) ]$$ (36)

and consequently

$$v(R) = 4 + 16\varepsilon + O(\varepsilon^2)$$ (37)

which shows that $v(R)$ is more sensitive than $v(Q)$ to an asymmetry in charge.

The $\Gamma$ measure is quite similar to $v(Q)$. Since $\frac{\<Q\>}{\<n_{ch}\>}=\varepsilon$ and $\<Q-\varepsilon \cdot n_{ch}\>=0$, equation (3.22) can be rewritten to yield

$$\Gamma = \frac{1}{\<n_{ch}\>} \mt{V}(Q-\varepsilon \cdot n_{ch}) =$$

$$= \frac{1}{\<n_{ch}\>} \left[\<Q^2\> + \varepsilon^2\<n_{ch}^2\> ... ...\> - \<Q\>^2 - \varepsilon^2\<n_{ch}\>^2 + 2\varepsilon\<Q\>\<n_{ch}\>\right] =$$

$$= \frac{1}{\<n_{ch}\>} \left[\mt{V}(Q) + \varepsilon^2\mt{V}(n_{c... ...] = \frac{1}{\<n_{ch}\>} \left[\mt{V}(Q) - \varepsilon^2\mt{V}(n_{ch})\right] =$$

$$= v(Q) - \varepsilon^2 v(n_{ch})$$ (38)

where the relation below was used.

$$\<Q \cdot n_{ch}\> = \sum_{n_{ch}}\Pi_{n_{ch}}\sum_{n_+}\Pi_{n_+}(2n_+-n_{ch})n_{ch} =$$

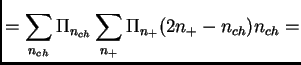$$= 2\sum_{n_{ch}}\Pi_{n_{ch}}n_{ch}\sum_{n_+}\Pi_{n_+}n_+ - \sum_{n_{ch}}\Pi_{n{ch}}n_{ch}^2 = (2p_+-1)\<n_{ch}^2\> = \varepsilon\<n_{ch}^2\>$$ (39)

If $\varepsilon=0$, (3.26) shows that $\Gamma$ is equal to $v(Q)$. Comparing with (3.15) it is seen that when using $\Gamma$ the $v(n_{ch})$ dependence is gone. The corresponding result for $\Gamma$ is

$$\Gamma = (1-p_a)(1-\varepsilon^2)$$ (40)

The $\nu _{dyn}$ measure, equation (3.23), can also be written

$$\nu_{dyn} = \left\<\left(\frac{n_+}{\<n_+\>}-\frac{n_-}{\<n_-\>}\right)^2\right\> - \left(\frac{1}{\<n_+\>}+\frac{1}{\<n_-\>}\right) =$$

$$= \frac{4}{\<n_{ch}\>^2} \left\<\left(\frac{n_+}{1+\varepsilon}-\... ...c{2}{\<n_{ch}\>} \left(\frac{1}{1+\varepsilon}+\frac{1}{1-\varepsilon}\right) =$$

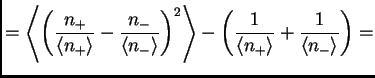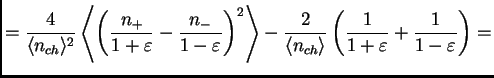$$= \frac{4}{\<n_{ch}\>} \left[ \frac{\left\<\left(\frac{n_+}{1+\va... ...1-\varepsilon}\right)^2\right\>}{\<n_{ch}\>} -\frac{1}{1-\varepsilon^2} \right]$$ (41)

and with charge symmetry, $\varepsilon=0$,

$$\nu_{dyn} = \frac{4}{\<n_{ch}\>} \left[v(Q)-1\right]$$ (42)

It can easily be shown that, in the stochastic scenario, $\nu_{dyn}=0$ and the result for $\nu _{dyn}$ corresponding to equations (3.15) and (3.28) is

$$\nu_{dyn} = -\frac{4}{\<n_{ch}\>} \cdot \frac{p_a}{1-\varepsilon^2}$$ (43)

For a given set of events this would yield a constant value, since $\<n_{ch}\>=p_a\<N_{ch}\>$. This value would be unaffected by an efficiency less than 100% [25], but would change when a background contribution is added, as will be seen in section 3.2.