Svenska:

Den här webbplatsen kan endast nås som arkivreferens. De officiella webbsidorna för avdelningen för partikelfysik finns på http://particlephysics.physics.lu.se

Sidan nedan slutar uppdateras fr.o.m. 2020-09-22 och uppfyller endast delvis tillgänglighetsdirektivet. Se tillgänglighetsredogörelsen

English:

The webpage you reached is made available for archiving purposes only. The official division of particle physics webpages can be found at http://particlephysics.physics.lu.se

The page below is not updated any longer since September 22, 2020 and does not conform completely to the accessibility regulation. See the accessibility statement

Luminosity

All processes in elementary particle physics are based on probabilities, as it is impossible to tell in advance what is going to happen in a specific e^-e⁺ collision. The probability for a specific process to happen is called its cross section, as it has the unit of m² (for practical reasons 1 barn= 10^-28m² is used instead). This can be schematically viewed as the electron and positron cover certain areas in space, and the total cross section for a collision is then the sum of these areas.

The probability for a collision is then the cross section area of the two particles ($\sigma$) divided by the total area of the beams ( 2$\pi$ ^. $\sigma_{x}^{}$ ^. $\sigma_{y}^{}$). Normally there is more than one particle in the beam, so this should be multiplied with the number of electrons(N^-) and positrons(N⁺) in the beam. The probability $\cal {P}$ for an event to happen and the collision rate per unit time $\cal {N}$ in a e⁺e^- collider is then:

$$\cal {P}$$ = $${\frac{N^+ N^- \sigma}{2 \pi \cdot \sigma_x \cdot \sigma_y}}$$        $$\cal {N}$$ = $${\frac{f N^+ N^- \sigma}{2N_b \cdot 2 \pi \sigma_x \sigma_y}}$$ = $$\cal {L}$$ ^. $$\sigma$$

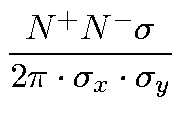
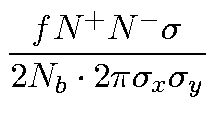In the second expression, f is the revolution frequency and N_b is the number of bunches in the beam. The definition of the luminosity ($\cal {L}$) appears at the end, and is thus defined as the interaction rate per unit cross section. An accelerator is mainly defined by two parameters, the energy of the beams and its ability to achieve high luminosity. As seen from the expression above, it is clear that it is important to keep the beam-width as small as possible and at the same time to pack as many electrons and positrons in each bunch as possible. Normally the luminosity is integrated over time and the natural unit for the integrated luminosity then becomes barn^-1.

In order to compare different experiments with each other it is essential to have a good luminosity measurement, so that the cross section for different processes is comparable. The beam parameters mentioned above are hard to measure with high enough accuracy, so instead the number of events in a process with a well defined cross section are counted. For this purpose elastic electron-positron scattering (Bhabhas) normally is used. This process has a well determined cross section (eq. 4.1) as well as a distinctly defined energy and momentum distribution.

$${\frac{d\sigma_0}{d\Omega}} {\frac{a^2}{16s}} {\frac{(3+cos^2\theta)^2}{sin^4\theta/2}}$$ (4.1)